文章编号：1296 / 更新时间：2024-12-30 10:48:05 / 浏览：次

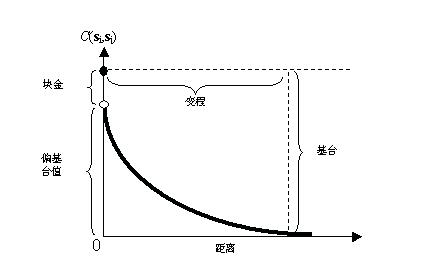
半方差函数是衡量投资组合风险的一种工具，它特别关注投资组合下行风险的程度。与标准差等衡量标准不同，半方差函数仅考虑收益率分布中的负收益率，这意味着它可以提供有关投资组合下行波动性的宝贵见解。

半方差函数公式

半方差函数的公式如下：

HS(x) = E[(R - μ)(R - μ)]其中：HS(x) 为目标半方差R 为投资组合的收益率μ 为投资组合的预期收益率

半方差函数模型

半方差函数模型是一个风险管理工具，可以帮助投资者评估投资组合的下行风险。该模型假设投资组合的收益率呈正态分布，并使用半方差函数来衡量投资组合分布的下半部分。

半方差函数模型的优点包括：

• 它可以识别投资组合中的资产之间的下行相关性。
• 它可以提供有关投资组合下行波动性的宝贵见解。
• 它相对容易解释和理解。

半方差函数模型的缺点包括：

• 它仅评估收益率分布的下半部分，不评估上半部分。
• 它依赖于正态分布假设，这可能对某些资产类别的收益率分布不准确。

半方差函数与标准差

半方差函数与标准差是衡量投资组合风险的两种最常用的衡量标准。它们是用不同的方法计算的，并且关注投资组合风险的不同方面。

标准差衡量投资组合收益率的总体波动性，包括正收益率和负收益率。半方差函数仅关注负收益率，这使其成为衡量投资组合下行风险的更准确的指标。

以下表格总结了半方差函数和标准差之间的主要差异：

半方差函数	标准差
仅考虑负收益率	考虑正收益率和负收益率
衡量下行风险	衡量总体波动性
正态分布假设	正态分布假设

半方差函数在投资组合管理中的应用

半方差函数在投资组合管理中有多种应用，包括：

• 资产配置：半方差函数可以帮助投资者选择具有较低下行风险的资产。
• 风险管理：半方差函数可以用来评估和管理投资组合的下行风险。
• 业绩评估：半方差函数可以用来评估投资组合经理的下行风险管理技能。

结论

半方差函数是一种有用的工具，可用于衡量投资组合的下行风险。通过仅考虑负收益率，半方差函数可以提供有关投资组合下行波动性的宝贵见解。半方差函数模型是一个风险管理工具，可帮助投资者评估投资组合的潜在损失，并做出明智的投资决策。

相关标签： 一种衡量投资组合风险的衡量标准、 半方差函数、 半方差函数模型、

本文地址：https://www.qianwe.com/article/1fcdb4d0459ec5fcd225.html

上一篇：反函数求导法则反函数求导法则证明...
下一篇：Excel中必备的八大常用函数excel中间横线怎...