指数函数的导数 (指数函数的导数推导过程)

文章编号：1363 / 更新时间：2024-12-30 11:38:56 / 浏览：次

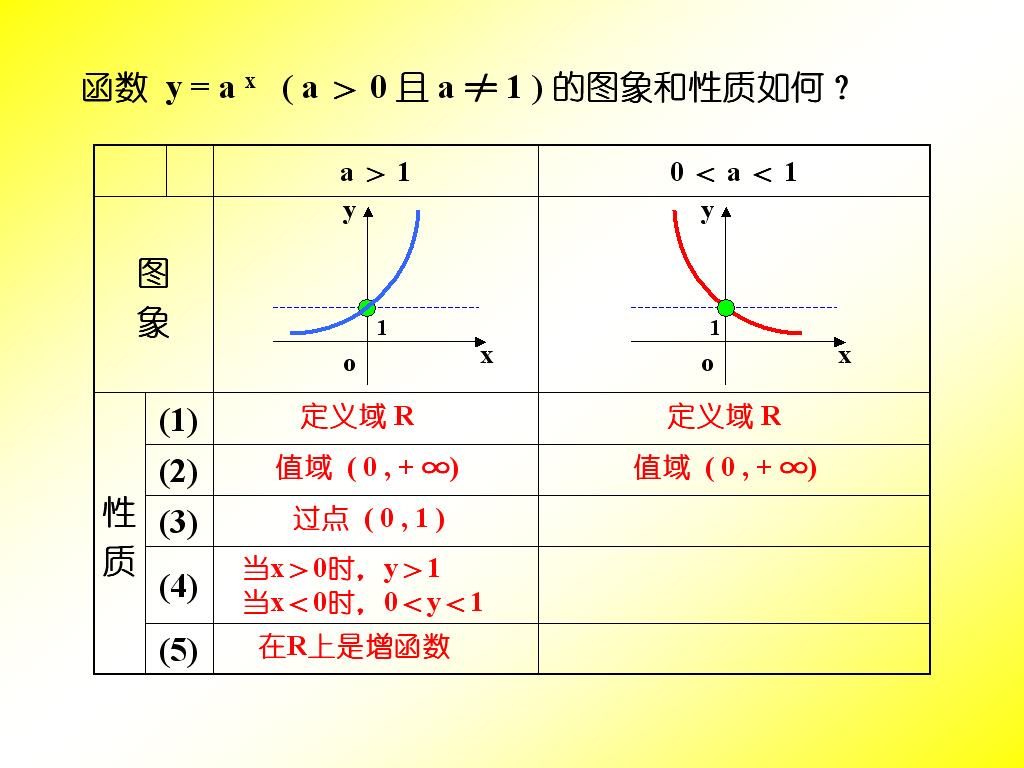
指数函数的定义

指数函数是形如 f(x) = a ^x 的函数，其中 a 是一个正实数（a > 0）。

指数函数的导数推导过程

为了求指数函数的导数，我们需要使用以下极限公式：```lim _{h → 0} (a ^h - 1) / h = ln(a)```其中 ln(a) 是以 e 为底的 a 的自然对数。使用这个公式，我们可以推导指数函数 f(x) = a ^x 的导数：```f'(x) = lim _{h → 0} [f(x + h) - f(x)] / h= lim _{h →03ex ln(a)```因此，指数函数 f(x) = a
^x
的导数为 f'(x) = a
^x
ln(a)。

特殊情况

对于自然指数函数 f(x) = e
^x
，导数为 f'(x) = e
^x
。这是因为 e = lim
_{a → ∞}
(1 + 1/a)
^a
，所以 ln(e) = 1。对于实底数 a = 1，指数函数为恒函数 f(x) = 1
^x
= 1，导数为 f'(x) = 0。

应用

指数函数的导数在微积分中有着广泛的应用，例如：求解微分方程求导数的连锁法则求极限积分

练习

以下是一些练习题，以帮助您理解指数函数的导数：1. 求导数：f(x) = 2
^x
2. 求导数：f(x) = e
^-x
3. 求导数：f(x) = 10
^x
+ 24. 求导数：f(x) = 2
^x
e
^-x

答案

1. f'(x) = 2
^x
ln(2)2. f'(x) = -e
^-x
3. f'(x) = 10
^x
ln(10)4. f'(x) = 2
^x
e
^-x
(ln(2) - 1)}
相关标签：指数函数的导数推导过程、指数函数的导数、

本文地址：https://www.qianwe.com/article/213e2e1d2d225b506eb2.html

上一篇：VLOOKUP函数的操作实例一步步指导您使用Exc...
下一篇：网游数据库收集整理和分析网游数据的宝库网...