文章编号：1294 / 更新时间：2024-12-30 10:46:10 / 浏览：次

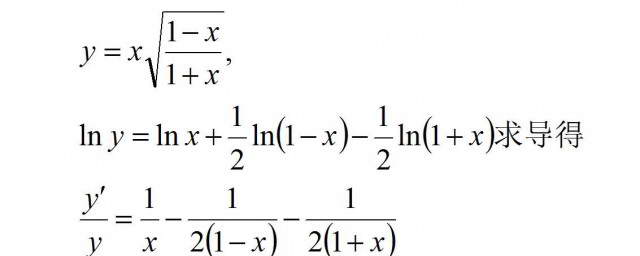
指数函数求导是微积分中一个常见的操作，它在科学、工程和经济学等领域有着广泛的应用。本文将介绍指数函数求导的基本原理，并提供详细的求导公式和具体步骤。

指数函数

指数函数是指以常数为底数，幂为自变量的函数。形式为：

f(x) = a ^x

其中：

• a 为正实数，表示函数的底数
• x 为自变量 ，化简为：

  f'(x) = lim _h→0 (a ^x (a ^h - 1)) / h

  当 h 趋于 0 时，a ^h 趋于 1，因此：

  f'(x) = lim _h→0 (a ^x (a ^h - 1)) / h = a ^x lim _h→0 (a ^h - 1) / h

  使用极限定义，lim _h→0 (a ^h - 1) / h = ln(a)，因此：

  f'(x) = a ^x ln(a)

  具体步骤

  为了求导指数函数 f(x) = a ^x ，可以按照以下步骤进行：

  1. 确定函数的底数 a
  2. 使用指数函数求导公式：f'(x) = a ^x ln(a)
  3. 将底数 a 代入公式，得到导数

  示例

  求导 f(x) = 2 ^x

  使用指数函数求导公式：

  f'(x) = 2 ^x ln(2)

  因此，f(x) = 2 ^x 的导数为 f'(x) = 2 ^x ln(2)。

  应用

  指数函数求导在以下领域有着广泛的应用：

  • 科学：如建模人口增长、放射性衰变和化学反应动力学
  • 工程：如分析电路行为、控制系统和流体动力学
  • 经济学：如建模经济增长、利率和股票价格

  结论

  掌握指数函数求导的基本原理对于理解微积分和解决实际问题至关重要。通过理解指数函数求导公式及其证明，并遵循具体的步骤，我们可以轻松求导任何指数函数。

相关标签： 指数函数求导公式、 掌握数学中的基本原理、 指数函数求导、

本文地址：https://www.qianwe.com/article/47090f7c5c5b31963e1e.html

上一篇：Excel中必备的八大常用函数excel中间横线怎...
下一篇：周期函数周期函数的八个基本公式...