欧拉函数:数学中的重要工具,用于计算小于给定整数的相对素数的数量 (欧拉函数数列的前10项)
文章编号:1184 /
更新时间:2024-12-30 09:17:44 / 浏览:次
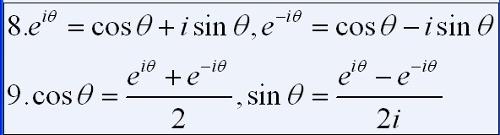
相关标签: 用于计算小于给定整数的相对素数的数量、 欧拉函数、 欧拉函数数列的前10项、 数学中的重要工具、
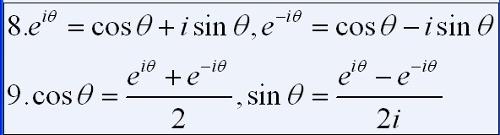
概述
欧拉函数,又称为欧拉φ函数,是一个数学函数,它计算小于给定正整数 n 的相对素数(又称互质数)的数量。换句话说,它计算与 n 没有公因子的正整数的数量。定义
欧拉函数 φ(n) 被定义为:φ(n) = {n-1, n 是质数{n(1 - 1/p_1)(1 - 1/p_2) ... (1 - 1/p_k), n 是合数其中 p_1、p_2、...、p_k 是 n 的质因数。性质
欧拉函数具有以下性质:φ(1) = 1如果 p 是质数,则 φ(p) = p-1如果 n = p_1^a_1 p_2^a_2 ... p_k^a_k,其中 p_i 是不同的质数,则 φ(n) = n(1 - 1/p_1)(1 - 1/p_2) ... (1 - 1/p_k)φ(mn) = φ(m) φ(n) 当 m 和 n 互质时φ(n) 总是偶数,除非 n = 2应用
欧拉函数在数论中有着广泛的应用,包括:计算线性同余方程的解求解二次回归的解构造伪随机数生成器在密码学中用于密钥生成和验证欧拉函数数列的前10项
欧拉函数数列的前10项为:1, 1, 2, 2, 4, 2, 6, 4, 6, 4计算欧拉函数
对于较小的数字,可以使用上面定义的公式手动计算欧拉函数。对于较大的数字,可以使用以下伪代码:```def phi(n):if n == 1:return 1if n == 2:return 1factors = []for i in range(2, n + 1):if n % i == 0:factors.append(i)result = nfor factor in factors:result = (1 - 1/factor)return int(result)```结论
欧拉函数是一个重要的数学工具,在数论、密码学和计算等领域有广泛的应用。理解欧拉函数及其性质对于解决各种数学问题至关重要。相关标签: 用于计算小于给定整数的相对素数的数量、 欧拉函数、 欧拉函数数列的前10项、 数学中的重要工具、
本文地址:https://www.qianwe.com/article/528e843a88fdf4804aa4.html
做上本站友情链接,在您站上点击一次,即可自动收录并自动排在本站第一位!
<a href="https://www.qianwe.com/" target="_blank">前卫目录网</a>
<a href="https://www.qianwe.com/" target="_blank">前卫目录网</a>

 人气排行榜
人气排行榜












 豫公网安备 41172402000154号
豫公网安备 41172402000154号