Gamma 分布密度函数：概率论中用于表示正偏数据的连续概率分布 (gamma分布的期望和方差)

文章编号：529 / 更新时间：2024-12-29 23:37:48 / 浏览：次
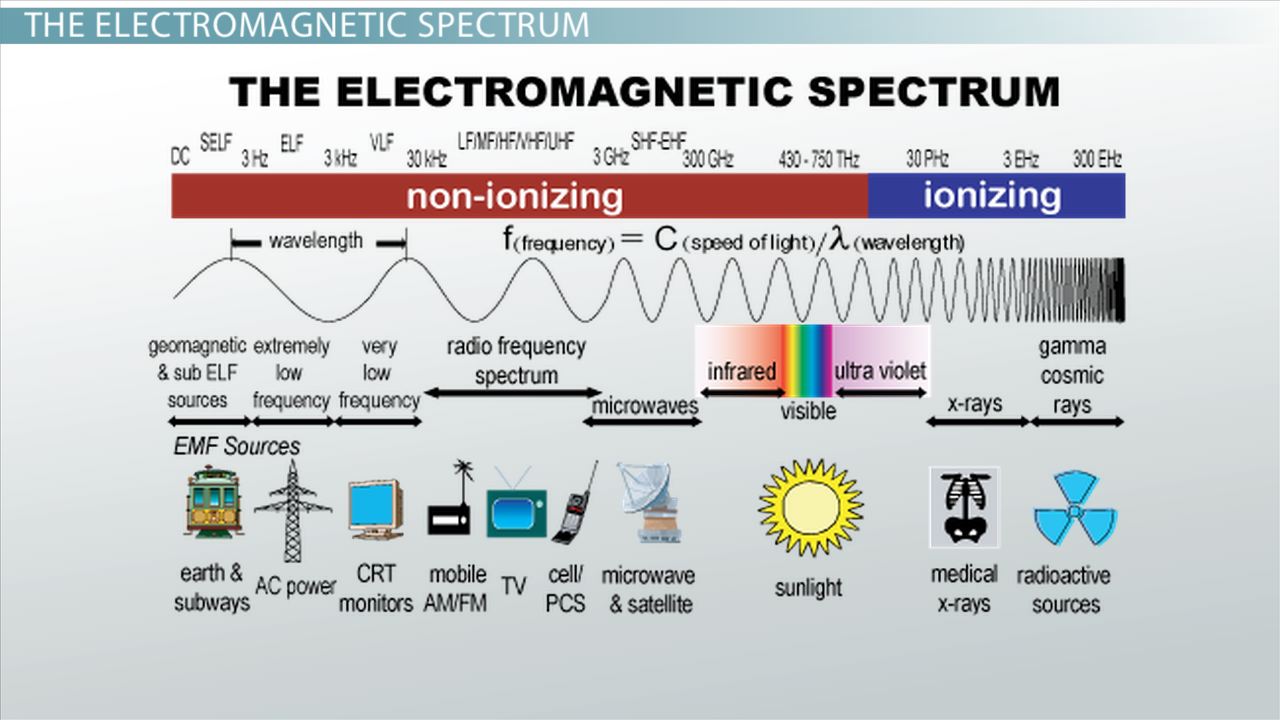
概率论中表示正偏数据的连续概率分布

Gamma 分布是一种连续概率分布，常用于表示正偏数据，即数据具有较长的右尾。

密度函数

Gamma 分布的密度函数定义如下：

$$f(x)= \frac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha-1} e^{-\beta x}$$

其中：

$\alpha$ 是形状参数，控制分布的形状。
$\beta$ 是速率参数，控制分布的尺度。
$\Gamma(\alpha)$ 是 Gamma 函数。

期望和方差

Gamma 分布的期望和方差分别为：

Gamma 分布是可加性的，这意味着如果 $X_1$ 和 $X_2$ 是独立 Gamma 分布随机变量，形状参数分别为 $\alpha_1$ 和 $\alpha_2$，速率参数分别为 $\beta_1$ 和 $\beta_2$，则 $X_1 + X_2$ 也服从 Gamma 分布，形状参数为 $\alpha_1 + \alpha_2$，速率参数为 $\beta_1 + \beta_2$。

应用

Gamma 分布广泛用于各种领域，包括：

金融：建模资产收益率的分布。
可靠性：建模组件或系统的故障时间。
保险：建模保险索赔的金额。
生物学：建模种群增长或衰减率。

生成 Gamma 分布随机数

在 Python 中，可以使用


 scipy.stats

模块生成 Gamma 分布随机数：


 import scipy.stats as stats设置形状和速率参数alpha = 5beta = 2生成 Gamma 分布随机数x = stats.gamma.rvs(alpha, beta, size=100)打印随机数print(x)

结论

Gamma 分布是一种适用于正偏数据的灵活概率分布。它具有许多有用的特性，例如可加性和与其他分布的关系。Gamma 分布在各种领域都有广泛的应用。
相关标签：分布密度函数、 Gamma、 gamma分布的期望和方差、概率论中用于表示正偏数据的连续概率分布、

本文地址：https://www.qianwe.com/article/82c13a7c15ae329b5019.html

上一篇：标签创建长标题标签创建长标怎么做...
下一篇：Java移位运算深入理解位操作和优化性能java...

发表评论

温馨提示

做上本站友情链接,在您站上点击一次,即可自动收录并自动排在本站第一位！
<a href="https://www.qianwe.com/" target="_blank">前卫目录网</a>

文章推荐

技术支持：前卫目录网