文章编号：1171 / 更新时间：2024-12-30 09:09:35 / 浏览：次

目录

1. 引言
2. 基本概念
3. 复变函数的极限与连续
4. 复变函数的导数
5. 复变函数的积分
6. 解析函数的性质
7. 柯西积分定理
8. 留数定理
奇点处留数的 2πi 倍。留数定理在求解积分、计算级数和解决物理问题中有着广泛的应用。

级数展开

泰勒级数

泰勒级数是复变函数在指定点周围的幂级数展开。它可以用来逼近函数的值，并且在解析函数的分析中非常有用。泰勒级数的系数由函数的导数在该点处计算得出。

罗朗级数

罗朗级数是复变函数在孤立奇点周围的幂级数展开。它可以用来逼近具有奇点的函数的值，并且在分析奇点附近的函数行为方面非常有用。罗朗级数的系数由函数的导数和留数计算得出。

共形映射

共形映射是复平面上两个区域之间的一一对应，它保持角度不变。共形映射在解决边界值问题、建模物理系统以及可视化复杂数据方面有着重要的应用。

积分变换

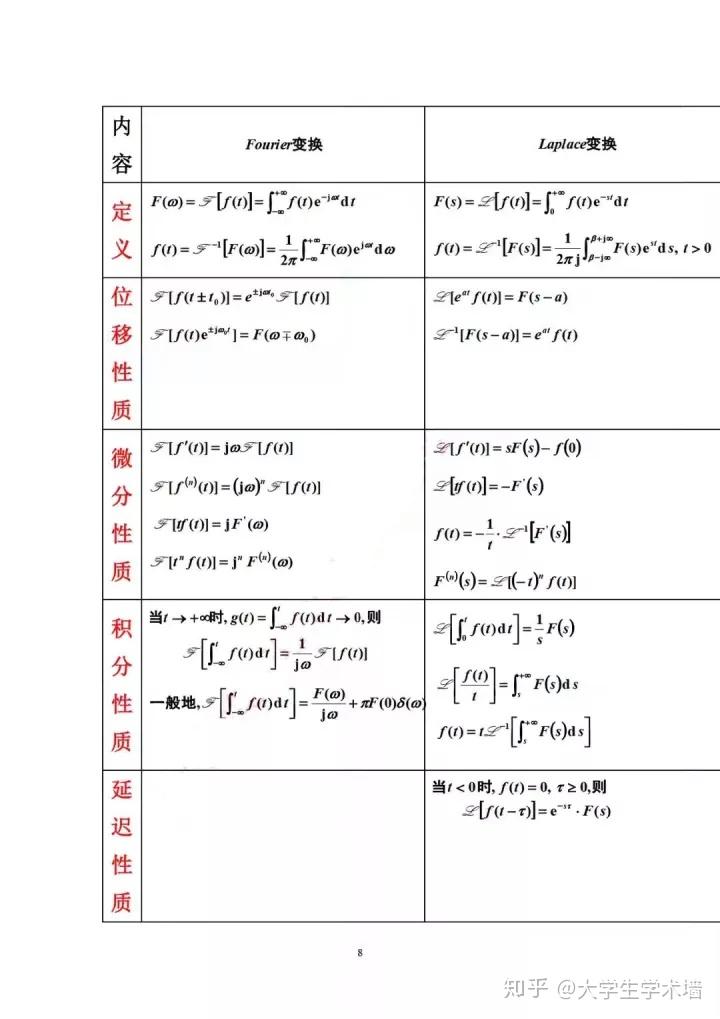
积分变换是将一个函数从一个函数空间变换到另一个函数空间的操作。积分变换在信号处理、图像处理和求解偏微分方程等领域有着广泛的应用。

拉普拉斯变换

拉普拉斯变换是一种积分变换，它将时域函数变换到复频域函数。拉普拉斯变换在求解微分方程、分析信号和系统稳定性方面非常有用。

傅里叶变换

傅里叶变换是一种积分变换，它将时域函数或空域函数变换到频域函数。傅里叶变换在信号处理、图像处理和光学等领域有着重要的应用。

应用

复变函数与积分变换在物理、工程和计算机科学等领域有着广泛的应用。

物理学

电磁学流体力学热力学量子力学

工程学

控制系统信号处理图像处理计算流体力学复变函数与积分变换在数学的其他分支，如数论、代数和拓扑学中也发挥着重要作用。

总结

复变函数与积分变换是数学中两大重要的分支，它们在解决许多科学和工程问题中起着至关重要的作用。复变函数的理论为理解和分析复杂现象提供了强大的框架，而积分变换则提供了对复杂信号和函数进行分析和处理的有效工具。通过理解这些概念和技术，研究人员和从业人员能够解决广泛的实际问题并推进各个领域的知识发展。

相关标签： 复变函数与积分变换第三版、 复变函数与积分变换、

本文地址：https://www.qianwe.com/article/9ec12f8255f84490d7d9.html

上一篇：回调函数异步编程中的利器回调函数异步执行...
下一篇：什么是数据库？B什么是平原...