对数函数求导规则详解 (对数函数求导公式)
文章编号:1355 /
更新时间:2024-12-30 11:31:39 / 浏览:次
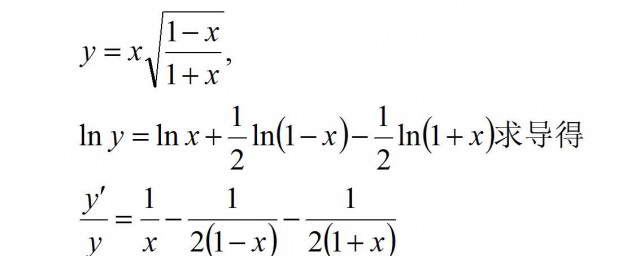
相关标签: 对数函数求导规则详解、 对数函数求导公式、
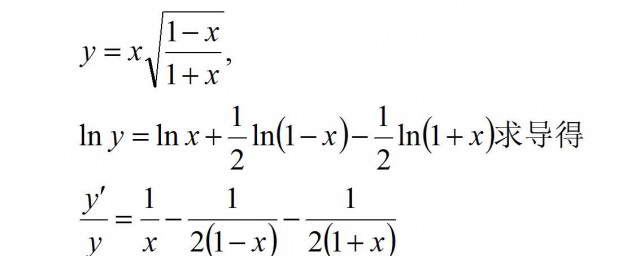
什么是对数函数?
对数函数是指数函数的反函数。它以指数的形式表示幂。例如,对于正数 \(a\) 和任何实数 \(x\),\(y = log_a(x)\) 等价于 \(a^y = x\)。对数函数的求导规则
对数函数的求导有多种规则,具体取决于对数的底数。自然对数 (底数为 e)
对于自然对数函数 \(y = ln(x)\),求导规则为:```y' = 1/x```其中 \(y'\) 表示 \(y\) 对 \(x\) 的导数。以 10 为底的对数函数
对于以 10 为底的对数函数 \(y = log_{10}(x)\),求导规则为:```y' = 1/(x\ln(10))```任意底数的对数函数
对于任意正实数 \(a\),\(a \neq 1\),以 \(a\) 为底的对数函数 \(y = log_a(x)\) 的求导规则为:```y' = \frac{1}{x\ln(a)}```证明
对数函数的求导规则可以通过利用指数函数的求导规则来证明。对于自然对数,令 \(u = ln(x)\)。那么,\(x = e^u\)。使用指数函数的求导规则,我们得到:```\frac{d}{dx}[x] = \frac{d}{du}[e^u]\frac{du}{dx}```即:```1 = e^u\frac{d}{dx}[u]```代回 \(u = ln(x)\),得到:```1 = x\frac{dy}{dx}```因此,对于自然对数,求导规则为 \(y' = 1/x\)。对于以 10 为底的对数函数,类似地,令 \(u = log_{10}(x)\)。那么,\(x = 10^u\)。使用指数函数的求导规则,得到:```\frac{d}{dx}[x] = \frac{d}{du}[10^u]\frac{du}{dx}```即:```1 = 10^u\ln(10)\frac{d}{dx}[u]```代回 \(u = log_{10}(x)\),得到:```1 = x\ln(10)\frac{dy}{dx}```因此,对于以 10 为底的对数函数,求导规则为 \(y' = 1/(x\ln(10))\)。对于任意底数的对数函数,证明类似。示例
求 \(y = log_2(x^2+1)\) 的导数。解:使用对以 2 为底的对数函数的求导规则,得到:```y' = \frac{1}{x^2+1}\frac{d}{dx}[x^2+1] = \frac{2x}{x^2+1}```因此,\(y' = 2x/(x^2+1)\)。应用
对数函数的求导规则在许多应用中都有用,例如:求解微分方程最优化积分总结
对数函数的求导规则是:自然对数 (底数为 e):\(y' = 1/x\)以 10 为底的对数函数:\(y' = 1/(x\ln(10))\)任意底数的对数函数:\(y' = 1/(x\ln(a))\)这些规则可以在各种应用中使用,例如求解微分方程、最优化和积分。相关标签: 对数函数求导规则详解、 对数函数求导公式、
本文地址:https://www.qianwe.com/article/ae08edaf97256c660bec.html
做上本站友情链接,在您站上点击一次,即可自动收录并自动排在本站第一位!
<a href="https://www.qianwe.com/" target="_blank">前卫目录网</a>
<a href="https://www.qianwe.com/" target="_blank">前卫目录网</a>

 人气排行榜
人气排行榜













 豫公网安备 41172402000154号
豫公网安备 41172402000154号