欧拉函数:了解数学中的重要概念 (欧拉阝函数)
文章编号:1268 /
更新时间:2024-12-30 10:26:20 / 浏览:次
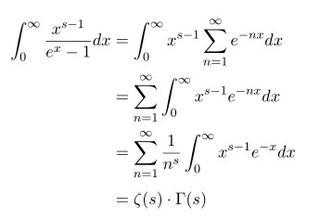
相关标签: 欧拉阝函数、 欧拉函数、 了解数学中的重要概念、
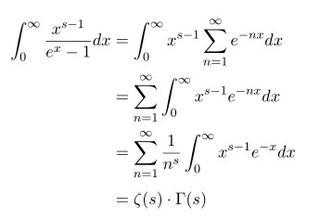
欧拉函数,又称欧拉φ函数,是一个在数论中非常重要的函数,它表示小于或等于给定正整数 \(n\) 的正整数中与 \(n\) 互质(即没有公因子)的整数的个数。
欧拉函数的定义
欧拉函数的定义如下:
$$\varphi(n) = |\{1, 2, 3, ..., n\} \cap \mathbb{Z}_n^|$$其中:\(\varphi(n)\) 是欧拉函数的值,表示与 \(n\) 互质的正整数的个数|\{1,2, 3, ..., n\} \cap \mathbb{Z}_n^| 表示集合 \(\{1, 2, 3, ..., n\}\) 和乘法群 \(\mathbb{Z}_n^\) 的交集的元素个数\(\mathbb{Z}_n^\) 表示模 \(n\) 的乘法群,即所有与 \(n\) 互质的正整数组成的集合欧拉函数的性质
欧拉函数具有以下几个重要的性质:性质 1: 若 \(p\) 是质数,则 \(\varphi(p) = p - 1\)。性质 2: 若 \(n = p_1^{a_1}p_2^{a_2}...p_k^{a_k}\) 其中 \(p_1, p_2, ..., p_k\) 是不同的质数,则 \(\varphi(n) = n(1 - \frac{1}{p_1})(1 - \frac{1}{p_2})...(1 - \frac{1}{p_k})\)。性质 3: 若 \(a\) 和\(b\) 是正整数,则 \(\varphi(ab) = \varphi(a)\varphi(b)\),当且仅当 \(a\) 和 \(b\) 是互质的。性质 4: 对于任意正整数 \(n\),\(\varphi(n)\) 是一个正整数。性质 5: \(\sum_{d|n}\varphi(d) = n\),其中求和范围是 \(n\) 的所有正因数。欧拉函数的应用
欧拉函数在数论中有着广泛的应用,其中一些重要的应用包括:求解模线性方程组: 欧拉函数可以用来求解模线性方程组 \(x \equiv a_i \pmod{m_i}\),其中 \(a_i\) 和 \(m_i\) 是正整数。计算 Carmichael数: Carmichael数是指大于 1 的正整数 \(n\),满足对于任意与 \(n\) 互质的正整数 \(a\),都有 \(a^n \equiv 1 \pmod{n}\)。欧拉函数可用来验证一个整数是否是 Carmichael数。计算本原根: 本原根是指模 \(n\) 的乘法群中一个生成元。欧拉函数可以用来计算模 \(n\) 的本原根。密码学: 欧拉函数在密码学中也扮演着重要的角色,例如在 RSA 加密算法中。示例
示例 1: 求 \(\varphi(12)\)。12 = 2 2 × 3由性质 2,\(\varphi(12) = 12(1 - \frac{1}{2})(1 - \frac{1}{3}) = 12(\frac{1}{2})(\frac{2}{3}) = 4\)示例 2: 求 \(\sum_{d|6}\varphi(d)\)。6 的正因数有 1、2、3 和 6。\(\varphi(1) = 1\),\(\varphi(2) = 1\),\(\varphi(3) = 2\),\(\varphi(6) = 2\)因此,\(\sum_{d|6}\varphi(d) = 1 + 1 + 2 + 2 = 6\)结论
欧拉函数是数论中一个非常重要的函数,它在各种数学问题和密码学中都有着广泛的应用。通过了解欧拉函数的定义、性质和应用,我们可以加深对数论和密码学的理解。相关标签: 欧拉阝函数、 欧拉函数、 了解数学中的重要概念、
本文地址:https://www.qianwe.com/article/ba1f9d72c8d305ce84c2.html
上一篇:Excel表格中强大的函数功能excel表格里面怎...
下一篇:数据库探针监视和优化数据库性能的终极指南...
做上本站友情链接,在您站上点击一次,即可自动收录并自动排在本站第一位!
<a href="https://www.qianwe.com/" target="_blank">前卫目录网</a>
<a href="https://www.qianwe.com/" target="_blank">前卫目录网</a>

 人气排行榜
人气排行榜














 豫公网安备 41172402000154号
豫公网安备 41172402000154号