余切函数:了解其性质、图形和在三角学中的应用 (余切函数讲解)
文章编号:847 /
更新时间:2024-12-30 04:56:57 / 浏览:次
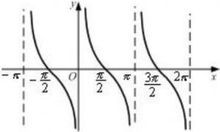
余切函数的图形
相关标签: 余切函数、 图形和在三角学中的应用、 余切函数讲解、 了解其性质、

什么是余切函数?
余切函数(记作 tan)是三角学中用于测量直角三角形中对边与邻边的比率的函数。在直角三角形中,对边是与所考虑角相对的边,邻边是与所考虑角相邻的边。
tan θ = 对边 / 邻边其中 θ 是所考虑的角度。余切函数的性质
余切函数具有以下性质:
- 余切函数是一个奇函数,这意味着当 θ 的相反数时,tan(-θ) = -tan θ。
- 余切函数的定义域是所有实数,除了奇数倍的 π/2。
- 余切函数的取值范围是 -∞ 到 ∞。
- 余切函数是周期函数,其周期为 π。
- 余切函数与正切函数互为倒数,即 tan θ = 1 / cot θ。
余切函数的图形
余切函数的图形是一个周期性的波浪形,其零点位于整数倍的 π。在奇数倍的 π/2 处,余切函数趋近于无穷大。在偶数倍的 π/2 处,余切函数趋近于零。
余切函数在三角学中的应用
余切函数在三角学中有很多应用,包括:
- 求边长:余切函数可用于求解直角三角形的边长。例如,如果知道一个角和一个边,则可以利用余切函数找到另外一个边。
- 求角:余切函数可用于求解直角三角形的角。例如,如果知道两个边,则可以利用余切函数找到其中一个角。
- 求三角形面积:余切函数可用于求解直角三角形的面积。例如,如果知道两个边,则可以利用余切函数找到三角形的面积。
- 单位圆:余切函数是单位圆上 x 坐标的函数。
- 其他三角学恒等式:余切函数可以用于推导其他三角学恒等式,例如和角公式和双角公式。
结论
余切函数是三角学中一个重要的函数,具有广泛的应用。了解余切函数的性质、图形和应用对于深入理解三角学至关重要。
相关标签: 余切函数、 图形和在三角学中的应用、 余切函数讲解、 了解其性质、
本文地址:https://www.qianwe.com/article/cd42bd8436fb80314608.html
做上本站友情链接,在您站上点击一次,即可自动收录并自动排在本站第一位!
<a href="https://www.qianwe.com/" target="_blank">前卫目录网</a>
<a href="https://www.qianwe.com/" target="_blank">前卫目录网</a>

 人气排行榜
人气排行榜









 豫公网安备 41172402000154号
豫公网安备 41172402000154号