简介伽马函数是一个非常有用的函数，在许多数学应用中都有用，例如，统计、概率、物理和工程，在MATLAB中，伽马函数可以使用gamma函数访问，用法gamma，x，函数计算伽马函数的值x，其中x可以是实数或复数，语法，```Y=gamma，X，```其中，X是一个实数或复数003e要计算伽马函数的值，可以使用gamma函数，例如，要计算...。

更新时间：2024-12-30 08:04:49

Gamma函数是一个将正实数映射到复数的函数，它在数学的许多领域中都有应用，包括概率论、统计学和物理学，Gamma函数可以通过多种方式定义，其中一种方法是使用积分，Γ，z，=∫77208504094032010362880Gamma函数表对于在各种应用中使用Gamma函数是很有用的，例如，Gamma函数可用于求解微分方程、计算概率分布...。

更新时间：2024-12-30 06:50:44

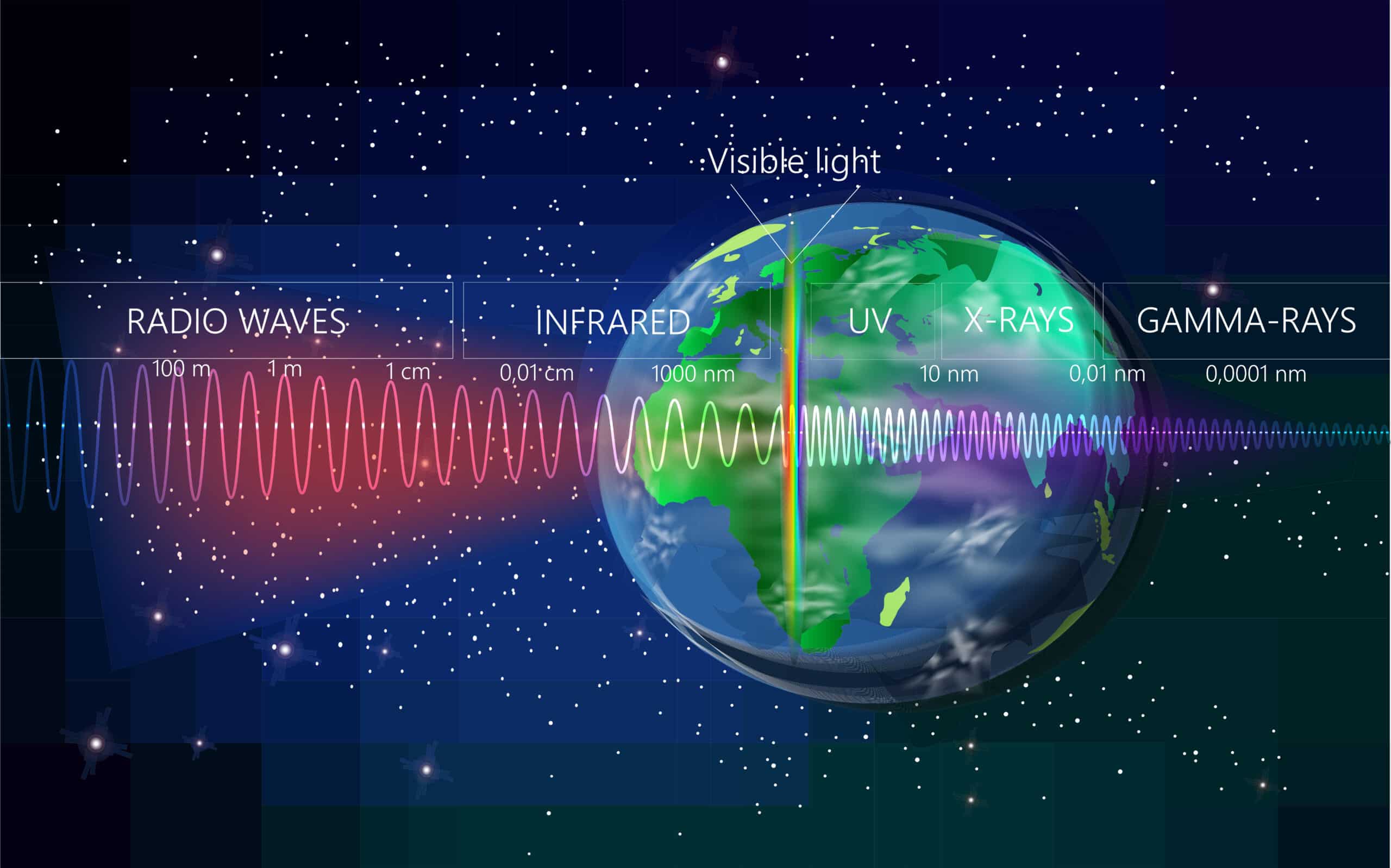
伽马分布是一种连续概率分布，其概率密度函数为，$$f，x，\alpha，\beta，=\frac，\beta^\alpha，\Gamma，\alpha，x^，\alpha，1，e^，\betax，$$其中，$x$是随机变量$\alpha$和$\beta$是正实数，称为形状参数和速率参数Gamma函数$\Gamma，\alpha，...。

更新时间：2024-12-30 00:01:40

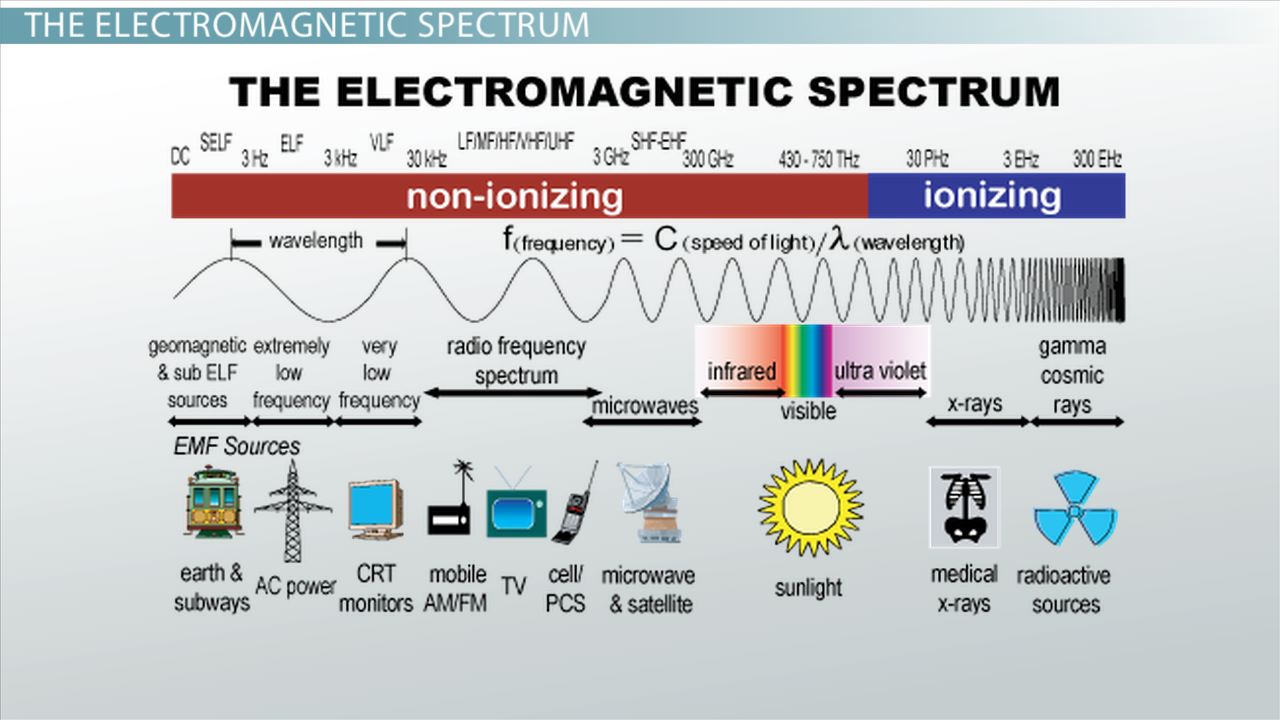
Gamma函数的定义Gamma函数是一个广义阶乘函数，它可以对任意复数或实数求值，它的定义如下，Γ，z，=∫0tz，1e，tdt其中z是复数或实数，Gamma函数的性质Gamma函数具有以下重要性质，解析性，Gamma函数在整个复平面上是解析的，但它在z=0和z=，1，2，...附近有极点，递归公式，Gamma函数满足以下递归公式，...。

更新时间：2024-12-29 22:36:47

Γ函数的定义Γ函数，又称伽马函数，是将正实数域上的正实数映射到复数域的一个特殊函数，它由欧拉在1729年提出，其定义为，Γ，z，=∫0tz，1e，tdt其中z是一个复数，Γ函数的性质解析性，Γ函数在整个复平面，除了负整数和零点，都是解析的，p>，Γ，z，n增殖公式，Γ，z，1，=zΓ，z，极点和零点，Γ函数在负整数处具有简单的极点...。

更新时间：2024-12-29 22:11:41

不完全伽马函数是一个特殊的函数，可以用于计算概率分布的累积分布函数，它在统计、数学和物理等不同领域都有应用，定义不完全伽马函数Γ辛普森积分法，使用特殊函数库中的内置函数，例如，在Python中的`scipy.special.gammainc`，结论不完全伽马函数是一个重要的数学函数，在不同领域都有着广泛的应用，通过理解其定义、性质和应...。

更新时间：2024-12-29 20:43:41

引言不完全Γ函数是数学中一个强大的工具，用于解决涉及复杂积分和概率分布的问题，它由莱昂哈德·欧拉在18世纪首次introduced，自此以来，它已在各种科学和工程领域中得到了广泛的应用，定义不完全Γ函数记为γ，a，x，，其中，a是一个正实数，称为函数的参数，x是一个非负实数，称为函数的积分上限，不完全Γ函数定义如下，$$\gamma，...。

更新时间：2024-12-29 20:22:49